Laboratoire 2¶

Dans ce laboratoire, vous allez mettre en pratique certaines notions d’algèbre, en particulier l’élimination de Gauss, et manipuler l’arithmétique modulaire ainsi que l’algèbre booléenne.

Note: Il existe bien sûr déjà des bibliothèques Python qui contiennent une implémentation de l’élimination de Gauss. Nous n’allons pas les utiliser, le but étant de vous amener à bien assimiler les concepts de base en réimplémentant votre propre version de cet algorithme.

Lights out¶

L’objectif consiste à implémenter le jeu Lights out. Celui-ci se joue sur une grille rectangulaire dont les cases peuvent être allumées ou éteintes. Initialement, la grille contient des valeurs aléatoires, comme dans cet exemple (les cases en bleu foncé sont celles qui sont allumées):

Lights out.

Pour résoudre le casse-tête, il faut arriver à éteindre toutes les cases qui sont allumées. Lorsque l’on clique sur une case, on inverse son état (on l’allume si elle est éteinte, et on l’éteint si elle est allumée), mais on inverse également l’état de toutes ses voisines. (On considère que deux cases sont voisines si elles possèdent un côté en commun.) Par exemple, en partant d’une grille où toutes les cases sont éteintes, si l’on clique sur les cases situées

à la troisième ligne et la quatrième colonne, et
en bas et à gauche de la grille,

on arrive à la situation suivante:

Règle du jeu.

Implémentation du jeu¶

La première étape consiste à rédiger un programme qui implémente ce jeu. Par simplicité, nous n’allons considérer que des grilles carrées, c’est-à-dire avec le même nombre \(n\) de lignes et de colonnes. Ce nombre \(n\) sera un argument du programme; par exemple, si l’on souhaite jouer sur une grille \(4 \times 4\), on invoquera le programme en lançant la commande python3 prog-6.py 4.

Procédure à suivre:

Le point de départ est le programme donné à la fin du guide rapide de Python et Pygame, que vous pouvez recopier dans un fichier que vous nommerez prog-6.py.
Les arguments fournis lorsque le programme est exécuté sont disponibles dans une liste appelée sys.argv (à condition de ne pas oublier l’instruction import sys au début de votre programme). Le premier argument de cette liste (sys.argv[0]) correspond au nom du programme. Si des arguments ont été spécifiés lors de l’invocation du programme, ces arguments sont placés dans les éléments suivants de la liste, sous la forme de chaînes de caractères.

Pour récupérer la valeur de \(n\), les mécanismes suivants peuvent vous être utiles:
- La fonction len(l) permet de récupérer le nombre d’éléments de la liste l.
- La fonction int(s) permet de convertir la chaîne de caractères s en un entier.
- Si l’utilisateur fournit un argument qui ne peut pas être converti en un entier, par exemple parce qu’il contient des caractères alphabétiques, l’évaluation de int(s) signalera une erreur. Il est possible de détecter cette erreur et d’y réagir en attribuant une valeur par défaut à \(n\) grâce à la construction suivante:
```
try:
    n = int(s)
except:
    n = 3
```
  Dans ce cas, l’instruction qui suit except: ne sera exécutée que si celle qui suit try: déclenche une erreur.
Vous avez donc à ce stade tous les éléments en main pour récupérer la valeur de \(n\). Une bonne stratégie est de forcer cette valeur à être supérieure ou égale à 3 (les grilles plus petites ne sont pas intéressantes) et inférieure ou égale à 10 (au-delà, il n’est pas facile pour l’utilisateur de manipuler la grille).
L’étape suivante consiste à représenter l’état courant de la grille (indiquant quelles sont les cases allumées et éteintes), et à lui donner une valeur initiale. Une solution naturelle consiste à utiliser une matrice d’entiers à \(n\) lignes et \(n\) colonnes: Une valeur égale à 1 désignera une case allumée, et une valeur égale à 0 une case éteinte.

Note: Une alternative tout à fait valable serait de définir une matrice de valeurs booléennes. Il n’est cependant pas certain que Python manipule ces valeurs plus efficacement que les entiers.

Pour créer cette matrice, vous pouvez exploiter les mécanismes suivants:
- L’expression [ f(i) for i in range(n) ] crée une liste comportant n valeurs, respectivement égales à f(0), f(1), …, f(n-1). Dans cette construction, f(i) peut être remplacée par n’importe qu’elle expression. Par exemple, [ 0 for i in range(n) ] retourne un vecteur possédant n éléments, tous nuls.
- Une matrice est un vecteur de vecteurs, ces derniers représentant les lignes de la matrice. Donc, l’instruction
  
  m = [ [ 0 for i in range(n) ] for j in range(n) ]
  
  place dans m une matrice à n lignes et n colonnes dont tous les élements sont nuls. Dans la suite du programme, l’expression m[r][c] correspondra à l’élément de cette matrice situé à la ligne r et à la colonne c.
- L’expression random.randint(0, 1) retourne un nombre entier tiré aléatoirement entre 0 et 1.
Maintenant que vous disposez d’une matrice représentant l’état courant de la grille, vous pouvez écrire une fonction qui dessine cette grille, ainsi que l’état allumé ou éteint de chaque case.

Vous pouvez vous inspirer des figures qui ont servi à illustrer les règles du jeu au début de ce tutoriel, qui ont été obtenues grâce aux paramètres suivants:
- La grille est centrée dans la fenêtre, et sa taille en pixels est égale aux trois quarts de la hauteur de la fenêtre.
- Les lignes noires servant à délimiter les cases ont une épaisseur de 10 pixels, et sont dessinées comme des rectangles.
Note: Après avoir dessiné la grille, n’oubliez pas d’invoquer pygame.display.flip() pour que cet affichage devienne visible!
Il ne reste plus qu’à mettre à jour l’état de la grille lorsque l’on clique sur une case. Pour ce faire, vous devez détecter l’évènement pygame.MOUSEBUTTONDOWN dans la boucle principale du programme, comme vous l’avez fait pour le programme affichant des fractales. Ensuite, il faut déterminer sur quelle case l’utilisateur a cliqué (en écartant les clics effectués en dehors de la grille), modifier l’état de la grille en fonction des règles du jeu, et afficher la grille mise à jour.

Votre programme devrait maintenant permettre de jouer à Lights out. Testez-le soigneusement, et déposez-le dans le répertoire centralisé sous le suffixe prog-6.py.

Résolution automatique¶

En mettant au point votre programme, vous avez probablement remarqué qu’il n’est pas si simple que cela de résoudre le casse-tête … (Y êtes-vous arrivé?)

Nous allons donc maintenant programmer un mode de résolution automatique permettant au programme de trouver à tous les coups une solution s’il en existe une.

En examinant le mécanisme de jeu, on voit facilement que:

L’ordre dans lequel on clique sur les cases n’a pas d’importance: Un clic sur la case \((r_1, c_1)\) suivi par un clic sur la case \((r_2, c_2)\) a exactement le même effet sur la grille qu’un clic sur la case \((r_2, c_2)\) suivi par un clic sur la case \((r_1, c_1)\).
Il est inutile de cliquer deux fois sur la même case, puisque le deuxième clic annule alors l’effet du premier.

En d’autres termes, pour résoudre le problème, il suffit de déterminer l’ensemble des cases sur lesquelles il faut cliquer (une seule fois!). Bien sûr, il est hors de question d’obtenir cet ensemble par une recherche exhaustive: Pour le problème à \(10 \times 10\) cases, il y a \(2^{100}\) solutions potentielles. Si votre ordinateur était capable d’en explorer un milliard par seconde (ce qui est déjà optimiste), le temps nécessaire à l’exploration de toutes ces possibilités serait environ 3000 fois plus grand que l’âge de l’univers!

Expression algébrique du problème¶

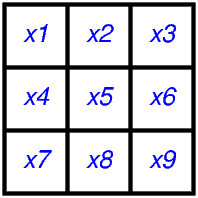
L’algèbre va nous permettre d’obtenir une solution plus efficace. L’idée consiste à associer une variable \(x_1\), \(x_2\), … à chacune des cases sur lesquelles on peut cliquer.

Par exemple, pour le problème \(3 \times 3\), on aura 9 variables \(x_1\), \(x_2\), …, \(x_9\) disposées de la façon suivante:

Variables associées aux cases.

Chacune de ces variables prendra la valeur 1 si l’on doit cliquer sur la case correspondante, et 0 sinon. Cela signifie que les valeurs de \(x_1\), \(x_2\), …, \(x_9\) désignent un ensemble de clics.

Nous allons maintenant chercher à répondre à la question suivante:

Si l’on effectue l’ensemble de clics représenté par \(x_1\), \(x_2\), …, \(x_9\), quelles sont les cases qui changeront d’état?

Pour répondre à cette question, il faut appliquer la règle du jeu qui dit qu’un clic affecte également les cases voisines, et compter le nombre de fois qu’une case change d’état: Si ce nombre est pair, la case restera inchangée. S’il est impair, l’état final de la case sera inversé.

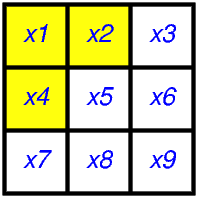
Par exemple, si l’on considère la première case de la grille (située en haut à gauche et associée à \(x_1\)), on voit qu’elle changera d’état chaque fois que l’on cliquera sur cette même case, mais aussi sur celle associée à \(x_2\) ou celle associée à \(x_4\). La situation est illustrée ci-dessous:

Clics affectant la première case.

En résumé, la première case de la grille changera d’état après la suite de clics \(x_1\), \(x_2\), …, \(x_9\) si la valeur de

\(x_1 + x_2 + x_4\)

est impaire, c’est-à-dire si l’on a

\(x_1 + x_2 + x_4 =_2 1\),

où \(=_2\) désigne l’égalité modulo 2.

Cela nous permet de traduire le problème en équations. Si la première case de la grille est initialement allumée, alors on doit avoir

\(x_1 + x_2 + x_4 =_2 1\).

pour qu’elle soit finalement éteinte après avoir effectué l’ensemble de clics représenté par \(x_1\), \(x_2\), …, \(x_9\).

Si cette case est initialement éteinte, on doit en revanche avoir

\(x_1 + x_2 + x_4 =_2 0\).

Nous allons résoudre le problème en

calculant une équation de ce type pour chaque case de la grille, et en
résolvant ensuite le système d’équations obtenu. Le résultat prendra la forme de valeurs pour \(x_1\), \(x_2\), …, \(x_9\) représentant l’ensemble des clics à effectuer pour résoudre le casse-tête.

Mécanisme de résolution automatique¶

Vous allez commencer par modifier le programme que vous avez conçu pour jouer à Lights out, de façon à y intégrer le mécanisme de résolution automatique. Le principe est simple: Lorsque l’utilisateur appuie sur la touche “S” (comme « Solve » ou « Smart »), le programme tente de résoudre le problème à partir de l’état courant de la grille. S’il trouve une solution, alors celle-ci sera affichée sous la forme d’un ensemble de cases sur lesquelles l’utilisateur doit cliquer.

Procédure à suivre:

Renommer votre programme en prog-7.py.
Dans la boucle principale, ajouter une détection des évènements de type pygame.KEYDOWN. Un tel évènement possède un champ key dont la valeur correspond au code de la touche qui a été pressée, par exemple pygame.K_s pour la touche “S”. Lorsque le programme détecte un appui sur cette touche, il doit invoquer une fonction resoudre() chargée d’effectuer les opérations suivantes:
1. Calculer un système d’équations représentant l’instance courante du problème.
2. Résoudre ce système en effectuant une élimination de Gauss.
3. Déterminer si le problème possède une solution et, le cas échéant, l’afficher.
Nous allons aborder séparément ces trois opérations. Avant cela, prenez la peine de vérifier que votre programme détecte correctement les appuis sur la touche “S” en remplaçant le corps de la fonction resoudre() par une simple instruction print("OK").

Calcul des équations¶

La première opération effectuée par resoudre() consiste à construire un système d’équations correspondant au problème. Comme expliqué précédemment, pour une grille \(n \times n\), ce système d’équations comprendra \(n^2\) variables (une par case de la grille), ainsi que \(n^2\) équations.

Ce système d’équations peut être représenté sous forme matricielle:

Chaque équation correspond à une ligne de la matrice \(M\) représentant le système.
Chaque variable correspond à une colonne de \(M\), avec une colonne supplémentaire pour le terme constant des équations.

Par exemple, dans le cas du problème \(3 \times 3\) discuté précédemment, nous avions obtenu l’équation

\(x_1 + x_2 + x_4 =_2 1\),

représentant le fait que la case associée à la variable \(x_1\) était initialement allumée. Pour rappel, les variables \(x_1\), \(x_2\) et \(x_4\) interviennent dans cette équation car un clic sur les cases correspondantes affecte l’état de la case qui nous intéresse (celle associée à \(x_1\)).

Cette équation sera donc représenté par la ligne

\([ 1\, 1\, 0\, 1\, 0\, 0\, 0\, 0\, 0\, 1 ]\)

de \(M\). Seuls les éléments figurant aux colonnes 1, 2, 4 et 10 sont non nuls, le dernier correspondant au terme constant de l’équation.

Note: Dans l’arithmétique modulo 2, les équations

\(x_1 + x_2 + x_4 =_2 1\)

et

\(x_1 + x_2 + x_4 + 1 =_2 0\)

sont équivalentes. Cela n’a donc pas d’importance de considérer que le terme constant est à gauche ou à droite du signe “\(=_2\)”.

Pour construire la matrice \(M\), vous allez répéter cette construction pour chaque case de la grille. Par exemple, voici comment calculer la deuxième ligne de cette matrice:

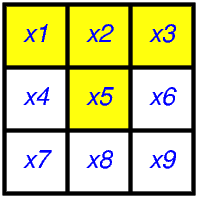
Cette ligne correspond à la variable \(x_2\), qui est associée à la case de la grille située en première ligne et deuxième colonne.
Cette case possède pour voisines les cases \(x_1\), \(x_3\) et \(x_5\):

Clics affectant la deuxième case.

L’équation pour cette case est donc

\(x_1 + x_2 + x_3 + x_5 =_2 e_{(1,2)}\),

où \(e_{(1,2)}\) représente l’état (allumé ou éteint) de la case située en première ligne et deuxième colonne (celle associée à \(x_2\)).
Cette équation se traduit en la deuxième ligne

\([ 1\, 1\, 1\, 0\, 1\, 0\, 0\, 0\, 0\, e_{(1,2)} ]\)

de \(M\).

Vous êtes donc maintenant à même de construire cette matrice. Le mieux est d’effectuer cette construction dans une fonction séparée prenant comme arguments l’état courant de la grille et la taille de celle-ci. La première opération de resoudre() sera donc d’appeler cette fonction. Ensuite, vous pouvez afficher la matrice \(M\) obtenue, de façon à vérifier que votre construction est correcte.

Notes:

Le code suivant permet d’afficher une matrice m de façon lisible:
```
for i in range(len(m)):
    print(m[i])
```
Pour une grille \(3 \times 3\), vous devriez obtenir le résultat suivant:

\[\begin{split}\begin{array}{cccccccccc} 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & ?\\ 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & ?\\ 0 & 1 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & ?\\ 1 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & ?\\ 0 & 1 & 0 & 1 & 1 & 1 & 0 & 1 & 0 & ?\\ 0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & ?\\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & ?\\ 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1 & ?\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 & ? \end{array}\end{split}\]

(La dernière colonne correspond à l’état courant de la grille.)

Elimination de Gauss¶

Cette opération constitue la deuxième étape de la fonction resoudre(). Elle a pour but de transformer le système d’équations représenté par la matrice \(M\) de façon à ce qu’il soit facile d’en extraire une solution.

Le principe consiste à transformer la matrice \(M\) en appliquant des opérations qui ne modifient pas l’ensemble des solutions du système. Dans notre cas, deux opérations sont suffisantes:

Permuter deux lignes de la matrice.
Ajouter une ligne de la matrice à une autre.

Lorsque l’on effectue cette dernière opération, il ne faut pas oublier que nous travaillons dans l’arithmétique des entiers modulo 2. Dans cette arithmétique, les règles de calcul sont particulières; on a ainsi:

\[\begin{split}0 + 0 &= 0\\ 0 + 1 &= 1\\ 1 + 0 &= 1\\ 1 + 1 &= 0.\end{split}\]

Si nous considérons que nos entiers représentent des valeurs booléennes (ce qui a un sens, vu qu’en arithmétique modulo 2 il ne peuvent prendre que deux valeurs), on voit que l’opération d’addition correspond en fait au ou exclusif (xor).

Vous pouvez donc définir deux nouvelles fonctions, chargées respectivement de

permuter deux lignes données de \(M\), et
d’ajouter modulo 2 une ligne donnée de \(M\) à une autre.

N’oubliez pas de tester que ces fonctions produisent le résutat attendu.

Nous pouvons maintenant rentrer dans le vif du sujet. L’élimination de Gauss vise à transformer \(M\) en une matrice échelonnée (voir cette référence pour une définition précise de cette propriété). Cette opération s’effectue de la façon suivante:

Appelons \(k\) le nombre de lignes déjà traitées. Initialement, \(k = 0\).

Note: Attention, dans cette discussion, nous considérons que la première ligne et la première colonne de la matrice sont celles d’indice 1. Dans votre implémentation, en revanche, n’oubliez pas que Python indice les élements d’une matrice à partir de 0!
On répète les opérations suivantes:
1. On recherche la première colonne de la matrice dont les éléments de ligne strictement supérieure à \(k\) ne sont pas tous nuls. On peut commencer cette recherche à la colonne \(k + 1\) (en d’autres termes, il n’est pas nécessaire d’examiner les colonnes de 1 à \(k\)).
  
  Si cette recherche échoue, alors l’élimination de Gauss est terminée. Dans le cas contraire, on note \(c\) l’indice de la colonne que l’on vient de trouver, et \(r\) la ligne du premier élément non nul dans cette colonne. L’élément de ligne \(r\) et de colonne \(c\) est appelé pivot.
2. Si le pivot n’est pas situé à la ligne \(k + 1\) (en d’autres termes, si \(r \neq k + 1\)), alors on permute les lignes \(r\) et \(k + 1\) de la matrice.
3. Le but est à présent que le pivot (qui est maintenant à la ligne \(k + 1\)) devienne le seul élément non nul de sa colonne. Pour ce faire, on examine toutes les lignes de la matrice sauf celle d’indice \(k + 1\). Pour chacune de ces lignes:
  - Si son élément situé à la colonne \(c\) est nul, alors on laisse cette ligne inchangée.
  - Si cet élément est égal à 1, alors on ajoute (modulo 2) à cette ligne celle d’indice \(k + 1\), en utilisant bien sûr la fonction que vous avez développée pour cette opération.
4. On incrémente \(k\).

Après avoir implémenté cet algorithme, vous pouvez tester qu’il fonctionne correctement en exécutant votre programme avec une grille \(3 \times 3\) (ce qui produit une matrice \(M\) à 9 lignes et 10 colonnes). Après élimination de Gauss, votre matrice devrait avoir pris la forme suivante:

\[\begin{split}\begin{array}{cccccccccl} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{(1,1)}\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & e_{(1,2)}\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & e_{(1,3)}\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & e_{(2,1)}\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & e_{(2,2)}\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & e_{(2,3)}\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & e_{(3,1)}\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & e_{(3,2)}\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & e_{(3,3)}, \end{array}\end{split}\]

où les valeurs \(e_{(1,1)}\), \(e_{(1,2)}\), …, \(e_{(3,3)}\) indiquent sur quelles cases il faut cliquer pour résoudre le problème. (Vérifiez que c’est bien le cas.)

Si le résultat obtenu n’est pas correct, vous devez instrumenter votre programme pour trouver la cause de l’erreur: Affichez à chaque étape les coordonnées du pivot et le résultat des opérations élémentaires (permutation et addition de lignes), et comparez-les aux résultats d’un calcul fait à la main.

Extraction d’une solution¶

Il est possible de démontrer que le problème \(3 \times 3\) possède toujours une solution. Ce n’est pas toujours le cas en général; par exemple, beaucoup de problèmes \(9 \times 9\) sont impossibles à résoudre.

Après avoir effectué l’élimination de Gauss, l’étape suivante consiste donc à déterminer si le problème admet une solution. Notons \(p\) le nombre de lignes de \(M\). Il y a trois possibilités:

La matrice \(M\) est composée d’une matrice identité \(p \times p\) et d’une colonne \(p + 1\) quelconque. (C’était le cas de notre exemple précédent.) Dans ce cas, le problème admet une solution unique, correspondant aux valeurs de la dernière colonne.
La partie supérieure gauche de la matrice \(M\) est composée d’une matrice identité \(q \times q\), avec \(q < p\). Les \(p - q\) dernières lignes de la matrice ne comportent que des éléments nuls.

Exemple (ne correspondant pas à une situation réelle):

\[\begin{split}\begin{array}{cccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 1\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\end{split}\]

Cette situation indique l’existence de plusieurs solutions. Dans l’exemple précédent, on a \(p = 9\) et \(q = 6\). Cela signifie que les trois variables \(x_7\), \(x_8\) et \(x_9\) peuvent prendre n’importe quelle valeur: Le problème admet donc \(2^3 = 8\) solutions. Les six premières lignes de \(M\) correspondent aux équations

\[\begin{split}x_1 &=_2 x_7 + x_9 + 1\\ x_2 &=_2 x_8 + x_9\\ x_3 &=_2 x_7 + 1\\ x_4 &=_2 x_7 + x_8 + 1\\ x_5 &=_2 x_8\\ x_6 &=_2 x_7 + x_8 + x_9\end{split}\]

qui montrent que les valeurs de \(x_1\), \(x_2\), …, \(x_6\) peuvent être facilement calculées à partir de celles de \(x_7\), \(x_8\) et \(x_9\).

(Rappel: En arithmetique modulo 2, faire passer un terme d’un membre à l’autre de l’équation ne modifie pas celle-ci.)

Si l’objectif est de trouver une solution au problème, la technique la plus simple est de choisir \(x_7 = x_8 = x_9 = 0\). L’ensemble des cases sur lesquelles il faut cliquer est alors donné, tout comme dans le cas précedent, par la colonne \(p + 1\) de la matrice.
La matrice comprend une ligne dont le seul élément non nul est celui de la dernière colonne.

Exemple (ne correspondant pas à une situation réelle):

\[\begin{split}\begin{array}{cccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 1\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 1 & 0 & 1\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\end{split}\]

Dans ce cas, le problème n’admet pas de solution. En effet, dans cet exemple, la septième ligne de la matrice représente l’équation

\(1 =_2 0\),

qui est clairement impossible.

Dans votre programme, écrivez une fonction qui détermine dans laquelle de ces trois situations se trouve la matrice \(M\) obtenue après l’élimination de Gauss. Cette fonction peut par exemple retourner une valeur booléenne indiquant si une solution existe ou non, ainsi qu’une liste de cases à cliquer dans le cas positif.

Affichage de la solution¶

La dernière étape consiste à visualiser la solution trouvée. Une possibilité est d’afficher un marqueur sur chacune des cases qui doit être cliquée, par exemple un petit point rouge:

Affichage de la solution.

Cette étape ne présente pas de difficulté particulière. La procédure à suivre est la suivante:

Ajouter à votre programme la définition d’une variable conseil contenant l’ensemble des cases sur lesquelles le programme conseille à l’utilisateur de cliquer. Initialement, cet ensemble est vide. Vous pouvez au choix représenter cet ensemble comme une liste de coordonnées ou de numéros de cases à cliquer, ou comme une matrice d’entiers ou de booléens dont chaque élément correspond à une case de la grille.
Modifier la fonction d’affichage de votre grille de façon à également afficher le contenu de conseil.
Lorsque l’utilisateur appuie sur “S”, si le programme trouve une solution, alors celle-ci doit être recopiée dans conseil.
Lorsque l’utilisateur clique sur une case de la grille:
- Si cette case figure dans le contenu courant de conseil, alors on l’y retire, de façon à ce que l’utilisateur ne soit pas amené à cliquer une deuxième fois sur cette case.
- Si cette case ne figure pas dans conseil, alors on l’y ajoute. (Une alternative serait, vu que l’utilisateur ne suit visiblement pas les conseils fournis par le programme, de réinitialiser conseil à l’ensemble vide.)

Après avoir implémenté cette procédure, déposez votre programme dans le répertoire centralisé, sous le suffixe prog-7.py.

Si vous avez atteint cette étape et que tout fonctionne comme prévu, bravo! Avec le mode automatique, êtes-vous maintenant capable de résoudre le casse-tête pour une grille \(10 \times 10\)? Si oui, cela signifie que votre programme vient de résoudre un système de 100 équations à 100 inconnues.